稳定婚姻问题，from ubc-vsp23，感觉确实是一个有趣的问题。

问题

问题本身：有n个男孩，n个女孩，每一个男孩有他对于所有女孩的排名，每一个女孩也有她对于所有男孩的排名，那么如何将他们配对呢？别tm说什么为什么一定要配对（ 图示：

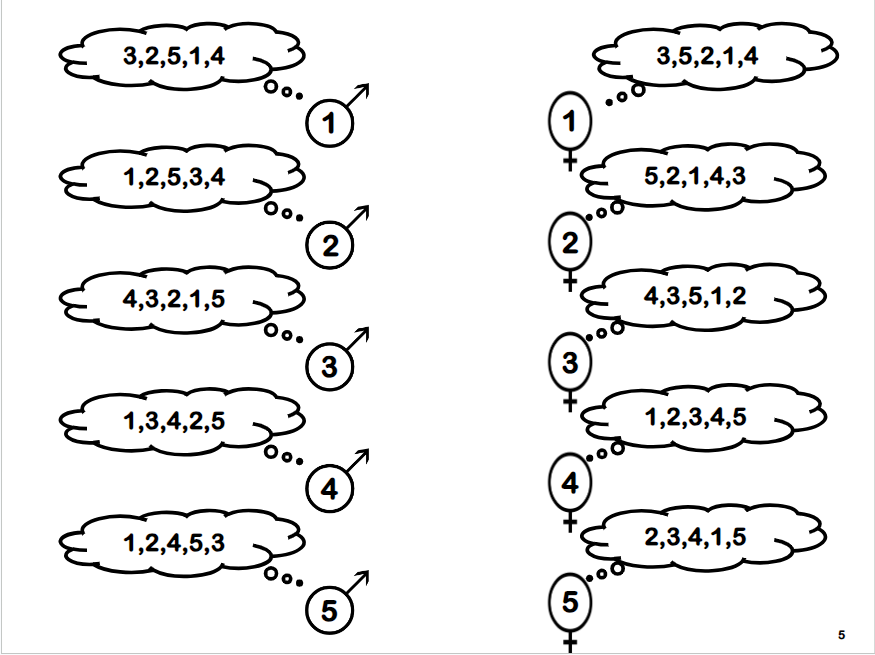
稳定婚姻问题.png

首先既然是稳定婚姻问题，我们得先定义出来什么是稳定，在婚姻问题中我们对稳定的定义是：不存在这样两队夫妻：她们彼此更喜欢另一对的另一半。emmm有点抽象，就是说男一和女一在一起，男二和女二在一起，如果男二和女一相互喜欢，那么这里的婚姻是不稳定的，不能出现这种情况。当然这样定义肯定会出现一个问题，这是第一个问题：每一个喜好列表的人都能找到稳定的配对吗？或者说，每一对情侣能找到一个保证稳定不分手的情况吗？这里有一个算法提出了一个解决方案：Gale-Shapley算法

Gale-Shapley算法

算法步骤如下:

  1. 初始时，所有的男性和女性都被标记为”单身”状态。
  2. 从未与女性提出过求婚的男性中，选择一个男性。
  3. 对于这个男性，按照他对女性的偏好顺序，从未被求婚过的女性中选择一位女性。
  4. 如果这位女性是”单身”状态，则接受男性的求婚，两人形成婚姻配对。
  5. 如果这位女性已经与其他男性形成婚姻配对，比较当前男性和已婚男性对女性的偏好，如果当前男性更受女性喜欢，则女性与当前男性解除婚姻关系，接受当前男性的求婚。
  6. 如果这位女性拒绝当前男性的求婚，男性继续尝试向下一位女性提出求婚。
  7. 重复步骤2-6，直到所有男性都提出过求婚。

这确实是一个很有意思的问题，多想想可以多理解一点东西。